Begleite mich auf eine Reise mit einem Zug. Der Zug wird gleichzeitig mit 1448 anderen Zügen losfahren. Du fährst zusammen mit dem erfolgreichsten Fondsmanager aller Zeiten. Am Ziel der Reise wird dein Zug ganz vorne landen und die anderen Züge hinter sich lassen.
Du stehst am Bahnsteig und hast die Auswahl aus 1449 Zügen. Alle Züge fahren in dieselbe Richtung, doch nur einer der 1449 Züge wird sicher vorne liegen.
Auf Gleis 8 von 1449 steht der Vanguard Express. Er fährt in der Geschwindigkeit der Weltwirtschaft und hat einen besonderen Gast an Bord: Mathe Matik, der erfolgreichste Fondsmanager aller Zeiten.
Alle anderen Züge versprechen dir schneller als der Vanguard Express zu sein, nur keiner kann es dir garantieren. Warum am Ende der Vanguard Express der schnellste sein wird, erläutere ich in diesem Beitrag.
Die Züge rollen los
Ich gehe Richtung Gleis 8, grüße den Lokführer John Bogle und steige in den Zug. Mir gegenüber sitzt Mathe Matik und erzählt mir interessante Fakten über die Fahrt.
Die Fahrt, so Matik, wird 100 Minuten dauern. Alle Züge fahren gleichzeitig mit einer Geschwindigkeit von 1km/h aus dem Bahnhof. Der Vanguard Express beschleunigt jede Minute um 7%. Nach einer Minute fährt er also 1,07 km/h, nach 20 Minuten 3,87 km/h und nach 50 Minuten 29,46 km/h.
Nach 100 Minuten hat der Vanguard Express auf knapp 868 km/h beschleunigt. Der Zinseszinseffekt sorgt also dafür, dass mit dieser Geschwindigkeit eine Fahrt zwischen Hamburg und München in ca. 1 Stunde möglich sein würde.
Nach ein paar Minuten sehe ich, dass ein paar Züge an uns vorbeifahren. Ich frage was es damit auf sich hat.
Matik erläutert: Alle anderen Züge beschleunigen jede Minute zufällig im Bereich zwischen 0% und 14%.
Einige Züge werden schneller sein als wir und andere werden langsamer sein. Ermittelt man die durchschnittliche Geschwindigkeit aller Züge, dann entspricht das exakt der Geschwindigkeit des Vanguard Express.
Ich sah ihn etwas verwirrt an und er ergänzte: Stell dir vor, es fahren nur drei Züge. Der Vanguard Express fährt 100 km/h und der schnellere Zug fährt 120 km/h. Wieviel muss dann der langsamere Zug fahren, damit alle durchschnittlich 100 km/h fahren?
Das war einfach! 80 km/h sagte ich stolz. Matik nickte zufrieden.
Nach 100 Minuten kam eine Durchsage. „Wir haben die Reisegeschwindigkeit erreicht. 611 Züge liegen vor uns und 817 Züge liegen hinter uns.“
Warum liegen immer mehr Züge hinter uns als vor uns?
Da ich die Strecke regelmäßig mit dem Vanguard-Express fahre, ist mir über die Zeit aufgefallen, dass stets mehr Züge hinter uns liegen als vor uns. Das kommt mir komisch vor. Im Schnitt müsste sich das doch die Waage halten, wenn die Beschleunigungen zufällig im Bereich 0% – 14% liegen.
Ich sprach Matik auf das Phänomen an. Er sagte: „Intuitiv nimmt man an, dass sich das die Waage halten muss.“ Mathematisch spricht hier aber der Zinseszins-Effekt ein gehöriges Wort mit.
Ich sah ihn an und schien ein ziemlich fragendes Gesicht zu machen.
Er bat mich, ihn auf ein Gedankenexperiment zu begleiten.
Stell dir vor es fahren zwei Züge. Der erste Zug beschleunigt mit 8,5% pro Minute. Der zweite Zug muss nun so beschleunigen, dass der Durchschnitt beider Züge eine Beschleunigung von 7% entspricht. Wie hoch ist dann Beschleunigung des zweiten Zuges?
Na, 5,5% fuhr es spontan aus mich heraus. Es erschien mir logisch, denn 5,5% plus 8,5% geteilt durch zwei ergibt doch 7%.
Gut, sagte Matik. Dann rechne mal aus wieviel Geschwindigkeit Zug 1 nach 100 Minuten hat. Ich tippte auf meinen Taschenrechner die Formel 1 * (1+8,5/100)^100. Das Display zeigt 3491 und ein paar Zerquetschte an. Nach 100 Minuten hat Zug 1 also eine Geschwindigkeit von 3491 km/h.
Ganz schön große Zahl dachte ich. Wie schnell muss nun Zug 2 fahren, damit beide eine Durchschnittsgeschwindigkeit von 868 km/h fahren? Ich nahm erneut meinen Rechner und tippte die Formel 868 * 2 – 3491 ein.
Das Ergebnis war negativ. Ich sah auf und sagte verwundert: Zug 2 muss ca. 1.756 km/h fahren – allerdings rückwärts…
Matik bestätigte meine Feststellung. Wenn wir davon ausgehen, dass ein Zug nicht rückwärtsfahren kann, wie erreiche ich dann trotzdem die Durchschnittsgeschwindigkeit?
Ich überlegte und kam zu dem Schluss, dass mehr als 1 langsamer Zug notwendig war, um die Durchschnittsgeschwindigkeit zu erreichen.
Im konkreten Beispiel braucht es 4 Züge mit einer Geschwindigkeit von jeweils 211 km/h, um auf die Durchschnittsgeschwindigkeit von 868 km/h zu kommen.
Das bedeutet für 1 Zug mit einer Beschleunigung von 8,5%, braucht es 4 Züge mit einer Beschleunigung von jeweils 5,5%, um auf die geforderte Durchschnittsgeschwindigkeit zu kommen.
Mit anderen Worten: Je schneller die Gewinnerzüge fahren, umso mehr muss das von den Verliererzügen kompensiert werden.
Durch Kosten fahren plötzlich alle Züge hinterher
Ein paar Wochen später saß ich wieder mit Matik im Vanguard Express. Matik erzählte mir, dass die Regeln geändert wurden, da die ständig wechselnde Beschleunigung nicht gut für die Gleise waren.
Deswegen wird bei den 1448 Zügen, die eine zufällig wechselnde Beschleunigung haben pauschal 1,5 Prozentpunkte abgezogen. Da der Vanguard Express kontinuierlich beschleunigt, werden dort nur 0,22 Prozentpunkte abgezogen.
Wird also eine Beschleunigung von 9% ermittelt, ist die Beschleunigung nach Abzug der 1,5 Prozentpunkte bei 7,5%. Bei 3% Beschleunigung, ergibt das nach dem Abzug 1,5%.
„Mit dieser Regeländerung werden wir nach 100 Minuten zu 99,9% die höchste Geschwindigkeit haben“, erklärte Matik.
Ich sah ihn an und fragte mich wie er sich so sicher sein konnte. Wir fuhren los und die Zugdurchsage hielt uns regelmäßig auf dem Laufenden.
Nach einer Minute erfolgte die erste Durchsage: „Es liegen bereits jetzt 60% der Züge hinter uns“. Nach 20 Minuten folgte die mit der zweiten Durchsage die Information, dass bereits 92% der Züge hinter uns fahren. Nach 50 Minuten waren es 99% und nach 100 Minuten waren 100% der Züge hinter uns.
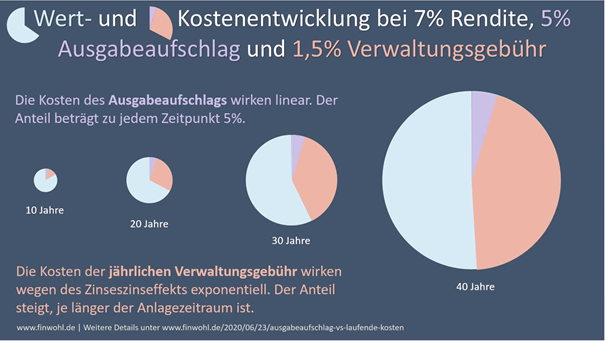
Ich sah Matik an und fragte: „Wie kann das sein?“. Matik erklärte mir, dass die Kosten – also der Abzug der 1,5 Prozentpunkte – ebenfalls vom Zinseszins-Effekt betroffen sind. Der Anteil der Kosten wächst über die Zeit nicht linear, sondern exponentiell an. Das führt dazu, dass die 1448 Züge über die Zeit immer weiter zurückfallen.

Deswegen kann die Masse der aktiven Fonds über die Zeit nicht erfolgreich sein
Matik zog eine Parallele zum Aktienmarkt. Genau wie bei den Zügen, verhält es sich am Aktienmarkt. Die Durchschnittsgeschwindigkeit aller handelbaren Aktien entspricht der Marktrendite. Wenn aktive Fonds oberhalb der Markrendite liegen, dann muss es aktive Fonds geben, die diese Überrendite finanzieren.
Bezogen auf die Marktrendite ist die Börse vor Kosten ein Nullsummenspiel. Sollte es besonders erfolgreiche aktive Fonds geben, dann müssten das sogar überproportional mehr nicht erfolgreiche Fonds finanzieren.
Hierbei ist es völlig unerheblich, ob die Renditen wie im Zugbeispiel zufällig zustande kommen oder ob es tatsächlich systematisch gelingen würde, den Markt zu schlagen. Die Wahrscheinlichkeiten bleiben dieselben. Nach 100 Runden wird es also nach Kosten zu 99,9% keinen aktiven Fonds mehr geben, der besser als die Marktrendite ist.
Nach Kosten ist es plötzlich ein Spiel, was die aktiven Fonds langfristig nicht gewinnen können. Die oben angenommen Kosten von 1,5% für aktive Fonds und 0,22% für den passiven Welt-ETF Vanguard FTSE All-World sind übliche Kosten für aktive und passive Produkte.
Sollte es wenige Fonds geben, die eine Systematik entdeckt haben und diese ausnutzen, dann werden sicherlich keine Privatanleger davon profitieren. Der hochgejubelte Medallion Fonds steht im Ruf diese Systematik entdeckt zu haben. Ein kleiner Wehrmutstropfen ist, dass er leider nicht von „normalen“ Anlegern erworben werden kann.
Gerd Kommer beschäftigt sich in seinem Blog-Artikel „Der beste Fonds aller Zeiten“ – oder auch nicht mit dem Medaillion Fonds.
Fazit
Ok, das Spiel kann nicht systematisch gewonnen werden. Was also tun?
Na, statt von den 1448 Zügen den vermeintlich schnellsten auszuwählen, kannst du dich einfach in den Vanguard Express setzen, die Mathematik für dich arbeiten lassen und dir gemütlich anschauen, wie die anderen Züge im Vergleich Minute um Minute langsamer werden.
Am Ziel wirst du dann auf Platz 1 oder in den Top 0,1% landen.
Der beste Fondsmanager aller Zeiten Mathe Matik ist zeitlos, verlangt keine Managementgebühr und folgt einfach universell geltenden mathematischen Gesetzmäßigkeiten.
Wie auch du davon profitieren kannst, beschreibe ich mit meinem minimal funktionsfähigen Portfolio.
Weitere Informationen zum Thema
Diese Beitrag inspirierte mich zu dem Zug-Beispiel: Einstein für Einsteiger – Die Relativitätstheorie einfach erklärt
Meine Artikel-Serie: 1 Welt-ETF reicht: Mit dieser Strategie wirst du langfristig garantiert zu den Gewinnern gehören
Mein Artikel: Zum Vatertag: Die Gewinnerstrategie für deine Geldanlage
Mein Artikel: Eine „kostenlose“ Provisionsberatung kann dich mehr als 6.000 Stunden zusätzliche Arbeitszeit kosten
Mein Artikel: Was ist besser? 5% weniger Ausgabeaufschlag oder 1 % weniger Verwaltungsgebühren?
Mein Artikel: Aktive und passive Anlagestrategien – eine Symbiose
 Mein Name ist Andree de Boer. Ich investiere seit Jahren passiv und prognosefrei mit der 1-ETF-Strategie erfolgreich in die Weltwirtschaft. Ich habe Erfahrung mit Immobilien, Immobilienfinanzierung und hole selbst aus der Riester-Rente eine überdurchschnittliche Rendite heraus.
Mein Name ist Andree de Boer. Ich investiere seit Jahren passiv und prognosefrei mit der 1-ETF-Strategie erfolgreich in die Weltwirtschaft. Ich habe Erfahrung mit Immobilien, Immobilienfinanzierung und hole selbst aus der Riester-Rente eine überdurchschnittliche Rendite heraus.
Ich verstehe unser Steuersystem und habe Erfahrungen mit der Optimierung von Abfindungen. Ich habe umfangreiches Wissen im Bereich staatliche Förderung. Ich zeige dir wie du mit der Rürup-Rente eine Vorsorge nach schwedischem Vorbild anlegen kannst.
Ich bin verheiratet und habe zwei Kinder und habe mich daher ausgiebig mit Anlagemöglichkeiten für Kinder und dem Thema Taschengeld auseinandergesetzt.
Ich kenne die Vor- und Nachteile unseres Rentensystems. Ich entziffere deine Renteninformation und durchleuchte deinen Altersvorsorgevertrag. Ich habe ausgerechnet warum sich bei der Geldanlage ab 50 eine freiwillige Einzahlung in die gesetzliche Rentenversicherung lohnen kann
Ich nutze den Vorteil eines Privatanlegers gegenüber institutionellen Anlegern und realisiere damit langfristig eine bessere Rendite als die Profis.
Auf meinem Blog berichte ich von meinen Erfahrungen und Recherchen zu allen Themen aus dem Bereich Privatfinanzen.
Mit meiner professionellen Coaching-Ausbildung zum FCM Finanz Coach kombiniere ich meine Kernkompetenzen und helfe Menschen nachhaltige Finanzentscheidungen zu treffen.
Auch wenn alle Konzepte eigenständig umgesetzt werden können, hat nicht jeder Zeit und/oder Lust sich um seine Finanzen zu kümmern. Für diese Menschen biete ich mein Finanzcoaching an.
Möchtest du einen ganzheitlichen Blick auf deine Finanzen, dann schau dir mein Angebot an und trete mit mir in Kontakt. Wir finden heraus, wie ich dir helfen kann.
Du möchtes auf dem Laufenden bleiben? Dann melde dich für den Newsletter an.